目录
快速导航-
教学纵横 | 五育视角下高中数学作业设计的实践案例
教学纵横 | 五育视角下高中数学作业设计的实践案例
-
教学纵横 | 深度学习视角下高中数学概念教学研究
教学纵横 | 深度学习视角下高中数学概念教学研究
-
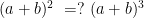
教学纵横 | 着力问题设计,助推学习进阶
教学纵横 | 着力问题设计,助推学习进阶
-
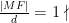
教学纵横 | 依托类比思维 重视问题引领 构建创生课堂
教学纵横 | 依托类比思维 重视问题引领 构建创生课堂
-
教学纵横 | 基于核心概念,丰富知识体系
教学纵横 | 基于核心概念,丰富知识体系
-
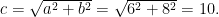
教例探微 | 合理转化错误资源 生动演绎课堂精彩
教例探微 | 合理转化错误资源 生动演绎课堂精彩
-
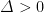
教例探微 | 概念再创造 实践真探究
教例探微 | 概念再创造 实践真探究
-
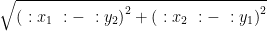
教例探微 | 以欧拉之名,寻e之源起
教例探微 | 以欧拉之名,寻e之源起
-
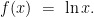
教例探微 | 一道课本习题的探究与反思
教例探微 | 一道课本习题的探究与反思
-

聚焦高考 | 2025年八省联考解几压轴题的解法探究及拓展
聚焦高考 | 2025年八省联考解几压轴题的解法探究及拓展
-
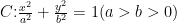
聚焦高考 | 再解豫皖名校联盟25届高三10月联考第18 题
聚焦高考 | 再解豫皖名校联盟25届高三10月联考第18 题
-
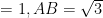
聚焦高考 | 2024年新高考I卷立体几何题解法再探究
聚焦高考 | 2024年新高考I卷立体几何题解法再探究
-

聚焦高考 | 从高考概率试题中的递推数列问题谈教材习题到高考试题的演变
聚焦高考 | 从高考概率试题中的递推数列问题谈教材习题到高考试题的演变
-
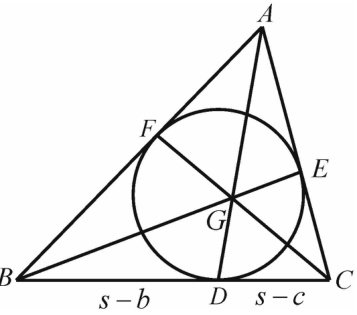
初数研究 | 涉及Gergonne线与 Nagel 线的部分性质
初数研究 | 涉及Gergonne线与 Nagel 线的部分性质
-
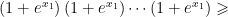
初数研究 | 一道以惠更斯问题为背景的多元函数最值问题的多解探究与推广
初数研究 | 一道以惠更斯问题为背景的多元函数最值问题的多解探究与推广
-
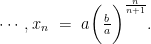
初数研究 | 余弦恒等式的变形及应用例析
初数研究 | 余弦恒等式的变形及应用例析
-
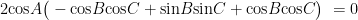
初数研究 | 双曲线内准圆的性质探究与应用
初数研究 | 双曲线内准圆的性质探究与应用
-
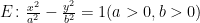
初数研究 | 对一类圆锥曲线双切线问题的推广研究
初数研究 | 对一类圆锥曲线双切线问题的推广研究
-
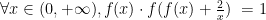
解题方法与技巧 | 基于数学抽象核心素养下的数学解题研究
解题方法与技巧 | 基于数学抽象核心素养下的数学解题研究
-
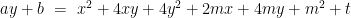
解题方法与技巧 | 例谈“等”与“不等”的转换应用
解题方法与技巧 | 例谈“等”与“不等”的转换应用
-
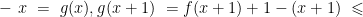
解题方法与技巧 | 从一道向量最值问题的求解探讨解题教学
解题方法与技巧 | 从一道向量最值问题的求解探讨解题教学
-
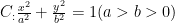
解题方法与技巧 | 一道椭圆中面积为定值试题的探究
解题方法与技巧 | 一道椭圆中面积为定值试题的探究
-
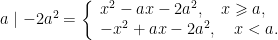
解题方法与技巧 | 基础与素养齐飞,多解共深度赏析
解题方法与技巧 | 基础与素养齐飞,多解共深度赏析
-
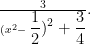
竞赛之窗 | 例析计数问题的解法
竞赛之窗 | 例析计数问题的解法
-
竞赛之窗 | 利用“先猜后证”思想解决一类整数条件问题
竞赛之窗 | 利用“先猜后证”思想解决一类整数条件问题





















 登录
登录